Number of Squares on a Chessboard

here is one really interesting puzzle what is the number of Squares on a Chessboard?

The first thing is why the answer is not just 64...

All the red squares in the above picture would count as valid squares, so we are asking how many squares of any dimension from 1x1 to 8x8 there are on a chess board. 

The key is to think how many positions there are that each size of square can be located... 

A 2x2 square, for example, can be located in 7 loactions horizontally and 7 locations vertically. ie in 49 different positions. Consider the table below... 

size	horizontal positions	vertical positions	positons
1x1	8	8	64
2x2	7	7	49
3x3	6	6	36
4x4	5	5	25
5x5	4	4	16
6x6	3	3	9
7x7	2	2	4
8x8	1	1	1
		total	204

In total there are 204 positions. this is the sum of the number of possible positions for all the different sized squares.

Formula For n x n Chessboard?

It's clear from the analysis above that the solution in the case of n x n is the sum of the squares from n² to 1²that is to say n² + (n-1)² + (n-2)² ... ... 2² + 1²

Mathematically that is written as follows:

The proof of the explicit solution is beyond the scope of this site, but if you want to look it up a mathematician would refer to it as 'the sum of the squares of the first n natural numbers.' The final answer is given by

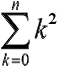
n³/3 + n²/2 + n/6

courtesy http://puzzles.nigelcoldwell.co.uk/twentyseven.htm